Rozwiązanie zagadki na odwrót

https://xpil.eu/i5k 📋

W zagadce pytamy ile jest w pudełku kulek każdego z trzech kolorów jeżeli szansa wylosowania trzech różnych kulek wynosi dokładnie 20%.

Piękno tej zagadki polega na tym, że w tego typu zadaniach na ogół znamy ilości kulek i szukamy prawdopodobieństwa. A tu - na odwrót.

Żeby to porządnie policzyć, musimy sobie rozbić losowanie kulek na trzy kroki (w rzeczywistości nie ma znaczenia czy będziemy te trzy kulki wyciągać na raz, czy jedna po drugiej).

Oznaczmy sobie ilości kulek każdego koloru przez x, y, z, a poszczególne kolory: A, B, C (dajmy na to, Amarant, Beż i Czerń). Szukamy prawdopodobieństwa zdarzenia, że każda wylosowana kulka będzie innego koloru.

Kulkę koloru A wyciągamy z prawdopodobieństwem x/100.

Potem kulkę koloru B: y/99 (bo w pudełku jest teraz o jedną kulkę mniej).

Koloru C: z/98.

A więc prawdopodobieństwo wylosowania trzech różnych kulek wynosi x/100*y/99*z/98, zgadza się?

Prawie.

Może przecież być tak, że najpierw wylosujemy B, potem C a na końcu A. Czyli nasze x/100*y/99*z/98 trzeba jeszcze przemnożyć przez 6, bo tyle jest różnych możliwych kolejności A, B, C.

Tak więc prawdopodobieństwo wylosowania trzech różnych kolorów wynosi (6xyz)/(100*99*98), po uproszczeniu xyz/161700. Z treści zadania wiemy, że prawdopodobieństwo to równe jest 20% czyli 0.2. A więc xyz/161700=0.2 czyli xyz/32340=1 czyli xyz=32340.

Wiemy też z treści zadania, że x+y+z=100.

I co dalej? Dwa równania, trzy niewiadome. Trochę słabo. A może nie?

Szukamy takich podzielników liczby 32340, których suma da dokładnie 100.

32340 dzieli się przez: 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 14, 15, 20, 21, 22, 28, 30, 33, 35, 42, 44, 49, 55, 60, 66, 70, 77, 84, 98, 105, 110, 132, 140, 147, 154, 165, 196, 210, 220, 231, 245, 294, 308, 330, 385, 420, 462, 490, 539, 588, 660, 735, 770, 924, 980, 1078, 1155, 1470, 1540, 1617, 2156, 2310, 2695, 2940, 3234, 4620, 5390, 6468, 8085, 10780, 16170, 32340.

Eliminujemy podzielniki większe od 100, zostaje: 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 14, 15, 20, 21, 22, 28, 30, 33, 35, 42, 44, 49, 55, 60, 66, 70, 77, 84, 98.

Trzeba teraz znaleźć wśród nich takie trzy, które sumują się do równej setki. A także wykazać, że żadne inne 3 nie sumują się do 100 (przy czym to drugie niekoniecznie, bo z treści zagadki wynika jasno, że jest tylko jedna taka kombinacja) .

Zauważamy, że średnia geometryczna tych trzech liczb wynosi niecałe 32 (pierwiastek sześcienny z 32340), a arytmetyczna - dokładnie 33 1/3 (bo suma=100) - obydwie te średnie są dość blisko siebie, a więc spodziewamy się, że nasze trzy liczby będą gdzieś bliżej środka stawki (a nie na brzegach). Na czuja eliminujemy więc skrajne wartości, zostaje nam: 20, 21, 22, 28, 30, 33, 35, 42, 44, 49, 55, 60, 66, 70.

20 odpada (bo pozostałe dwie muszą dawać sumę 80, nie ma takiej pary), z tego samego powodu odpada 55, 60, 66 i 70.

Zostaje: 21, 22, 28, 30, 33, 35, 42, 44, 49.

Teraz już łatwo. Metodą prób i błędów (pamiętając, że liczby muszą leżeć wokół 32-33) znajdujemy trójkę: 21, 35, 44.

Sprawdzamy: (21/100 * 35/99 * 44/98) * 6 = 0.2

Zgadza się!

Na wszelki wypadek powinniśmy jednak sprawdzić wszystkie możliwości, bo na czuja to sobie można robić różne inne rzeczy, ale nie matematykę 😉 Odpalamy Excela...

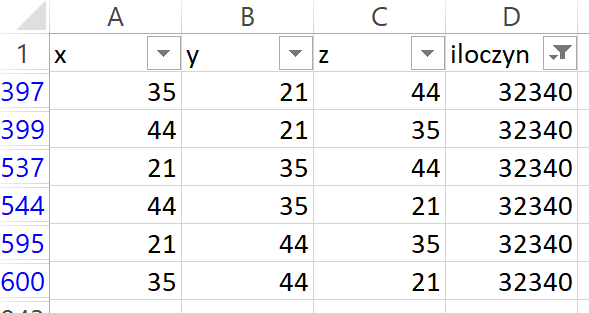
Jeżeli ktoś chce spróbować samemu, oto formuły, których użyłem:

Brzydzisz się Excelem? Można to samo w Pythonie:

for x in range(1,100):
    for y in range(x, 100):
        z = 100 - x - y
        if z > y:
            iloczyn = x * y * z
            if iloczyn == 32340:
                print(x, y, z)

Wynik:

21 35 44

Wszystko się zgadza.

A jak Wam poszło?

1Najpierw odezwał się Krzysiek, którego rozumowanie było poprawne z wyjątkiem pierwszego kroku - mianowicie przyjął on, że prawdopodobieństwo wylosowania trzech różnych kulek wynosi x/100*y/99*z/98 (zapomniał przemnożyć przez sześć). Wyszło mu więc, że zadanie nie ma rozwiązań, a więc - pomimo całkiem zgrabnego skryptu w Pytonie (plus za znajomość biblioteki Fractions) - pudło.

2Potem dostałem wiadomość od Waldka, który nie mógł wysłać rozwiązania standardowym formularzem (jakiś problem techniczny), więc skorzystał z formularza kontaktowego:

Liczby kulek oznaczmy: x, y, z. Dla wszystkich możliwości wylosowania trzech kolorów: 6xyz/(100*99*98)=0,2 stąd xyz=32340=2*2*3*5*7*7*11. Z tych cyferek trzeba ułożyć liczby x, y, z o sumie 100. Po kilku minutach otrzymałem: 3*7=21, 5*7=35, 2*2*11=44.

Waldek, 2021

Odpowiedź nie dość, że poprawna, to jeszcze bardzo zwięzła. Gratuluję!

Sprawdziłem formularz - noż kurdę, wszystko działa. Pewnie coś po stronie Waldka.

3Kolejnym rozwiązującym był Rozie, któremu formularz też nie działał, więc skorzystał z e-maila. Rozie wysłał odpowiedź ni z gruchy ni z pietruchy - chętnie poznam tok rozumowania (błędny, ale interesujący).

Sprawdziłem formularz po raz drugi. Spróbowałem z peceta i z telefonu. Znów wszystko działa. Ki czort?

4Jako czwarty odezwał się... Krzysiek! Coś mu zdecydowanie nie pasowało, przespał się z problemem i nazajutrz przysłał poprawne rozwiązanie wraz ze szczegółowym obliczeniem - z silniami, permutacjami, rozkładem na czynniki pierwsze i Wogle. Pogratulować zawziętości!

Przy okazji Krzysiek uspokoił mnie, że formularz do wysyłania rozwiązań jednak działa. Panowie Waldek i Rozie, obstawiam, mają coś nagmerane po swojej stronie. Ewentualnie miało miejsce jakieś chwilowe ugięcie czasoprzestrzeni. Czy coś...

https://xpil.eu/i5k 📋