Zagadkę o wyznaczaniu maksymalnej długości drogi startującej z narożnika kwadratowego stołu kuli bilardowej zanim uderzy ona w bandę po raz trzeci można ugryźć na kilka sposobów. Na przykład rozrysować sobie kilka wariantów (nie ma ich aż tak znowu wiele) i dla każdego z nich wyznaczyć długość drogi za pomocą trygonometrii, a zaraz potem maksimum tej długości za pomocą rachunku pochodnych. Albo zasymulować komputerowo (metoda zadziała, bo w zagadce narzucamy precyzję odpowiedzi: 4 miejsca po przecinku to nie tak znów wiele).
Ale można i bez używania trygonometrii czy w ogóle komputerów. Skoro bowiem kula zawsze odbija się od bandy idealnie pod tym samym kątem, pod którym pada, możemy sobie postawić wzdłuż każdej bandy wyimaginowane lustro i wtedy okaże się, że kula po trafieniu w bandę leci dalej prosto (tzn. jej lustrzane odbicie, ale do wyliczeń to bez różnicy). I to samo robimy z drugim odbiciem. W efekcie dostajemy następującego cósia:
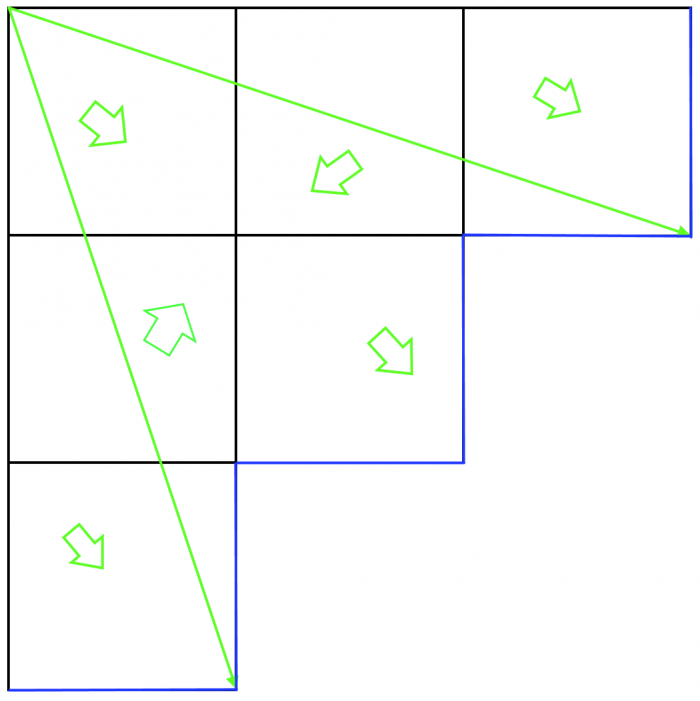
Bila startuje z górnej lewej części obrazka. Cienkie zielone strzałki pokazują punkty najbardziej odległe od startowego narożnika. Niebieskie linie to bandy po trzecim uderzeniu. Dla lepszego zobrazowania szerokie zielone strzałki pokazują faktyczny (zgrubny) kierunek ruchu kuli po kolejnych odbiciach.
Widać, że aby uzyskać maksymalną odległość trzeba celować w punkt znajdujący się dokładnie w 1/3 długości bandy. Co prawda zgodnie z warunkami zadania nie da się wycelować dokładnie w 1/3 długości bandy, bo to by oznaczało dokładne trafienie w narożnik po dwóch odbiciach, ale ponieważ możemy trafić dowolnie blisko tego narożnika, sytuacja nie zmienia się zbytnio (celujemy na przykład w 1000001/3000000 bandy i już). Przekątna prostokąta 1 na 3 metry ma długość \( \sqrt{3^2+1}\) czyli 3.1623 (po zaokrągleniu do czterech miejsc po przecinku) i to jest poprawna odpowiedź.
A jak Wam poszło?
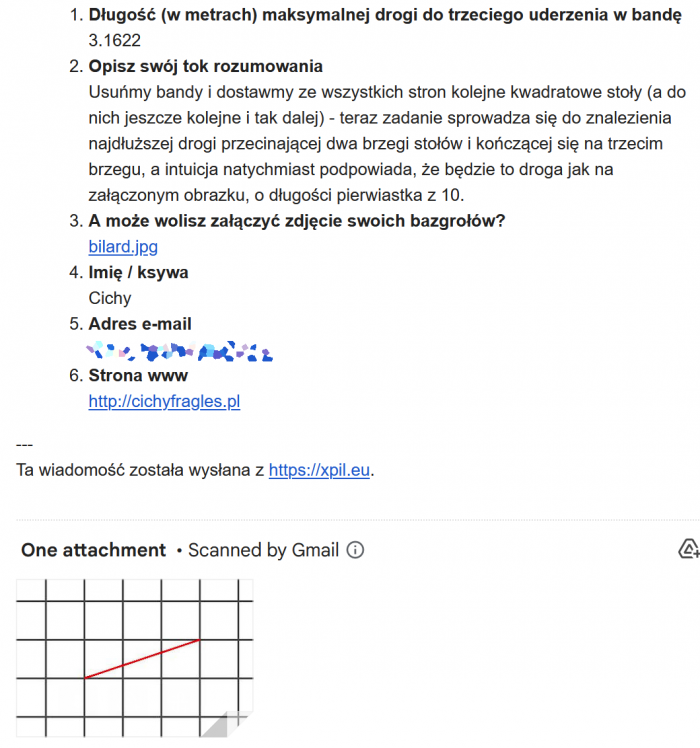
1W chwilę po opublikowaniu zagadki swoje rozwiązanie nadesłał Cichy - całkiem podobne do mojego. Cichy sugeruje dostawienie dookoła kolejnych stołów i usunięcie band, a następnie liczenie przez ile krawędzi przeleci kula. Podejście jak najbardziej poprawne, jednak Cichy walnął się przy zaokrąglaniu ostatniej cyfry dziesiętnej (pierwiastek z dziesięciu to 3.16227766017... - a więc zaokrąglając do 4 miejsc po przecinku dostajemy 3.1623). Ale nie bądźmy zbyt upierdliwi, w końcu wspomniał on również w komentarzu, że chodzi o \(\sqrt{10}\). Przymykam oko i zaliczam.
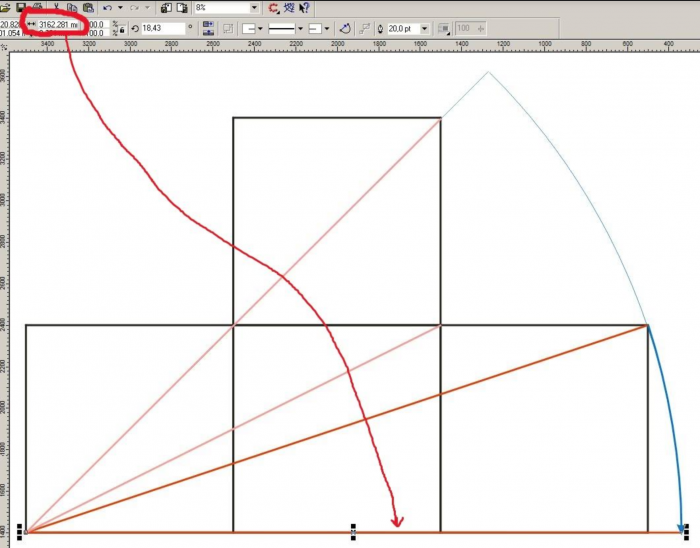
2Również tego samego dnia, pod wieczór, swoje inżynierskie rozwiązanie nadesłał Waldek, który wypiął się na moje pierwiosnki pierwiastki i jakby nigdy nic machnął rysunek poglądowy w Corelu - i też mu wyszło 3.1622. Waldek wprawdzie nie wspomniał o pierwiastku z dziesięciu i już miałem z szatańskim "HA!" odrzucić jego odpowiedź, ale potem zauważyłem, że na jego zrzucie ekranu widać wynik do sześciu miejsc po przecinku, więc się zamknąłem. Zaliczam.

3Nazajutrz rozwiązanie nadesłał Tywan, który jako pierwszy z rozwiązujących nie walnął się przy zaokrągleniach. Naturalnie, zaliczam.

Potem była chwila ciszy i nadszedł MDSM (Międzynarodowy Dzień Sprawdzania Mikrofonów).

4Kolejnym rozwiązującym był Piotr, który nie przemyślał sprawy do końca:
"Najdłuższy dystans kula może przebyć w kwadracie o boku 1m jest przekątna o długości 1.41 pi razy drzwi. Więc najdłuższy dystans przed trzecim odbiciem kuli wynosi dwa najdłuższe dystanse,czyli 2.82."
-- Piotr
Nie zaliczam. Mógłbym co prawda przyjąć, że drzwi są równe 0.1786 i wtedy podwojone pi x drzwi x 1.41 dałoby poprawny wynik, ale zmierzyłem swoje drzwi i mi wyszło, że się jednak nie zgadza.
5Rzast podesłał rozwiązanie posiłkując się rozwiązaniem jednej z poprzednich zagadek tu publikowanych. W dodatku potraktował on słowo "bazgroły" dosłownie i załączył... zdjęcie swoich bazgrołów 🙂 Zaliczam, na piątkę z plusem (w czasach kiedy chodziłem do szkoły skala była czterostopniowa, od 2 do 5, więc piątka z plusem to wynik poza skalą).


Tymczasem proszę o odświeżenie swoich umiejętności komputerowych, albowiem wkrótce pojawi się tutaj następna (niezbyt trudna) zagadka, która będzie - prawie na pewno - wymagała odrobiny programowania, a przynajmniej operowania karkuszem[1].
[1] Mój ulubiony neologizm na arkusz kalkulacyjny.
Mleko się rozlało, ale można trochę podywagować.
xpil w formularzu zadania: „z dokładnością do czterech miejsc po przecinku”
xpil w rozwiązaniu: „po zaokrągleniu do czterech miejsc po przecinku”
Czyli jak?
Najpierw pozaokrąglajmy, gdyż tu rozegrała się batalia o kartofle:
– Jeżeli zaokrąglę wynik na czwartym miejscu po przecinku 3,1623, to otrzymam dokładne jedynie trzy liczby po przecinku – źle, miały być cztery.
– Jeżeli zaokrąglę liczbę na piątym miejscu po przecinku 3,16228 to otrzymam… pięć cyfr. Też źle.
– Poza tym takie, czy inne zaokrąglanie, choć matematycznie poprawne, jest niezgodne z warunkiem z formularza.
Prawidłowy zapis z dokładnością do czterech cyfr po przecinku to 3,1622…, z kropkami oznaczającymi pominięty ciąg dalszy (formularz chyba nie akceptował takiego zapisu, więc pozostało bez kropek).
Chciałbym się pokłócić, ale chyba nie za bardzo jest o co. Można *obciąć* cyfry po czwartej (i wtedy mamy 3.1622) albo *zaokrąglić* do czterech miejsc po przecinku (i wtedy jest 3.1623). Ja mam w głowie zakodowane, że określenie „z dokładnością do N miejsc po przecinku” oznacza pozostawienie N-1 cyfr po przecinku bez zmian a N-tą można podnieść o jeden (chyba że jest dziewiątka, wtedy przeniesienie, wiadomo), o ile N+1 jest równa 5 lub więcej. O ile kojarzę są jeszcze jakieś bardziej przekombinowane systemy ustalania tej ostatniej N-tej cyfry w zależności od jej parzystości, używane w bankowości, żeby dla N+1==5 się zaokrąglało w miarę tak samo często w górę jak i w dół (dokładniejsza analityka ponoć), ale to już osobny temat.
Tak więc pisząc w formularzu zagadki „…z dokładnością do 4 miejsc po przecinku” miałem na myśli zaokrąglenie do czterech miejsc po przecinku, nie obcięcie.