Postawiona niedawno zagadka o prostopadłościanach nie jest wcale aż tak trudna, jak mogłoby się na pierwszy rzut oka wydawać. Kwestia - jak zwykle - doboru narzędzi.
Z zagadką zmierzyło się trzech Czytelników, jeden był całkiem blisko poprawnej odpowiedzi, drugi podał prawidłowe rozwiązanie, a trzeci nawet pokazał jak do tego rozwiązania dojść analitycznie. Szacun!
Można napisać sobie pętelkę w Pythonie czy innym C i po ludzku posprawdzać poszczególne kombinacje aż do długości krawędzi, dajmy na to, 1000. To tylko miliard kombinacji, prościzna.
Ale można też spróbować ugryźć zagadnienie zębem algebry i tak też dziś uczynimy.
Pokazana tu metoda w zasadzie nie różni się od tej w komentarzach pod zagadką - jest po prostu nieco lepiej uporządkowaną jej wersją.
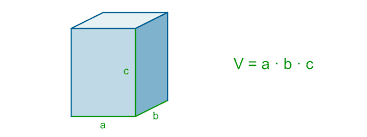
Objętość prostopadłościanu o bokach długości a, b, c wynosi abc.
Pole powierzchni całkowitej to 2ab+2ac+2bc.
Szukamy takich naturalnych a, b i c, dla których jedno równa się drugiemu:
\(abc=2ab+2ac+2bc\tag{1}\)Przyjmijmy dodatkowo, że a oznacza zawsze najdłuższą krawędź, c - najkrótszą, a b tę pomiędzy. Czyli:
\(a \geq b \geq c\tag{2}\)A skoro a i b to dwa najdłuższe boki, w takim razie ab jest nie mniejsze niż ac lub bc. A więc wiemy na pewno, że:
\(2ab+2ac+2bc \leq 2ab+2ab+2ab\)czyli
\(2ab+2ac+2bc \leq 6ab\).Sumę po lewej stronie możemy - zgodnie z (1) - zastąpić przez abc. Tak więc mamy:
\(abc \leq 6ab\)dzielimy obydwie strony przez ab i dostajemy zaskakująco nieoczywiste:
\(c \leq 6\tag{3}\)No proszę. Okazuje się, że najkrótsza krawędź prostopadłościanu spełniającego warunki zagadki nie może być dłuższa niż 6. To bardzo mocno zawęża nam poszukiwania. Sprawdźmy sobie teraz poszczególne warianty, zaczynając od c=6.
\( c=6 \)
Jeżeli w (1) przyjmiemy c=6, po uproszczeniu dostaniemy \(ab=3a+3b\) czyli \((a-3)(b-3)=9\). Ponieważ c jest nie większe niż a lub b, powyższą równość da się spełnić wyłącznie dla \(b=c=6\) czyli sześcianu o krawędzi 6. Pierwsze rozwiązanie to \((6, 6, 6)\).
\( c=5 \)
Tu mamy \(3ab=10a+10b \le 20a\), czyli \(b \le 6\). Ponieważ jednak \(b \ge c\), wystarczy tylko sprawdzić dla \(b=5\) lub \(b=6\). Okazuje się, że zadziała tu tylko kombinacja \( (10, 5, 5) \) i to jest nasze drugie rozwiązanie.
\( c=4 \)
Przy czwórce ilość kombinacji rośnie. Z (1) dostajemy \(ab=4a+4b\) czyli \((a-4)(b-4)=16\). 16 możemy rozłożyć na \( 16 \cdot 1 \) lub \( 8 \cdot 2 \) lub \( 4 \cdot 4 \), z czego dostaniemy \((20,5,4), (12,6, 4), (8, 8, 4)\). To już łącznie pięć rozwiązań. Zobaczmy co się dzieje dla mniejszych c.
\( c=3 \)
Dla c=3 dostajemy: \(ab=6a+6b\) co po przekształceniu daje \((a-6)(b-6)=36\). Liczbę 36 możemy przedstawić jako iloczyn dwóch liczb na pięć sposobów: \(36 \cdot 1, 18 \cdot 2, 12 \cdot 3, 9 \cdot 4, 6 \cdot 6\), co daje nam pięć kolejnych rozwiązań: \((42,7,3)\), \((24,8,3) \), \( (18,9,3) \), \( (15,10,3) \), \((12,12,3)\).
\(c < 3\)
Dla c=1 oraz c=2 równość (1) nie ma rozwiązań, a więc wygląda na to, że znaleźliśmy wszystkie możliwe kombinacje: \((6,6,6)\), \((10,5,5)\), \((20,5,4)\), \((12,6,4)\), \((8,8,4)\), \((42,7,3)\), \((24,8,3)\), \((18,9,3)\), \((15,10,3)\), \((12,12,3)\)
Najwyższy prostopadłościan ma krawędź o długości 42, co nie może być przypadkiem.
Inna ciekawostka: żaden z tych dziesięciu prostopadłościanów nie mieści się w całości we wnętrzu żadnego z pozostałych.
Na zakończenie dodam jeszcze, że skoro w dwóch wymiarach mamy dokładnie dwa takie prostokąty, a w trzech wymiarach - 10 prostopadłościanów, to może w wyższych wymiarach też jest jakieś ograniczenie?
Okazuje się, że i owszem. Czterowymiarowy hiperprostopadłościan, którego trójwymiarowa "powierzchnia boczna" równa się czterowymiarowej "objętości" bryły można skonstruować na 108 sposobów, przykładowo (3, 7, 78, 91). W pięciu wymiarach istnieją 2892 takie bryły, a w sześciu dobrze ponad ćwierć miliona (dokładnie 270332). Natomiast w siedmiu wymiarach... nie wiadomo. Nie udało się jeszcze ustalić ani czy taki limit istnieje, ani ile miałby on wynosić, dla brył o wymiarowości powyżej 6.
Jacyś chętni?
Jeżeli chcesz do komentarza wstawić kod, użyj składni:
[code]
tutaj wstaw swój kod
[/code]
Jeżeli zrobisz literówkę lub zmienisz zdanie, możesz edytować komentarz po jego zatwierdzeniu.